|
Introducción
Cluster Analysis 
Cluster analysis is a type of multivariate analysis technique that can be applied in many fields: from computer science, medicine and biology, from archaeology to marketing, whenever it is necessary to classify a large amount of information into distinguishable groups.
Objetivo 
El análisis cluster (o de conglomerados) se utiliza para agrupar unidades estadísticas (individuos, objetos, plantas, etc) que tienen características comunes y asignarlas a categorías no definidas a priori.
Los grupos (clusters) formados deben ser internamente lo más homogéneos posible (similitud intra-cluster) y lo más heterogéneos entre ellos (disimilitud inter-cluster).
Tipos de variables 
En el análisis clulster (o de conglomerados) se puede emplear:
- variables cuantitativas , es decir, numéricas ;
- variables cualitativas, que presentan modalidades (como género, nivel de educación, estado civil, etc.)
Análisis Clúster
Matriz de similitud (o Matriz de distancia) 
matriz de distancia D es útil para saber cuántas unidades estadísticas son diferentes entre sí, y es determinante para la elección de las variables a considerar.
La matriz de distancia, de dimensiones n×n , es una matriz simétrica que tiene valor 0 en la diagonal mayor, ya que la distancia entre un punto y él mismo es cero.
Antes de crear la matriz de distancia se debe estandarizar la matriz de partida; de este modo cada variable tendrá el mismo peso que las demás.
Para obtener la matriz de distancia D es necesario calcular las distancias entre los puntos.
Dependiendo del tipo de variable con la que se esté trabajando -cuantitativa o cualitativa-, estas distancias se pueden calcular de diferentes formas.
|
Variables cuantitativas:
- Distancia euclidea, sensible a valores atípicos.
- Distancia Manhattan, muy robusta.
|
|
Variables cualitativas:
Se tienen en cuenta las frecuencias, se crea la matriz de similitud y se calculan las concordancias y discrepancias entre las opciones.
Dos tipos de índices de similitud:
- Zubin, para variables simétricas binarias.
- Jaccard , para variables asimétricas binarias.
|
Creación de clústers 
Hay varias reglas de clustering (o métodos de vinculacion o linkage).
Para crear clusters podemos elegir entre los siguiente métodos de vinculación :
- Vinculación mínima o simple
- Vinculación completa
- Vinculación media o promedio
Vinculación minima o simple :
Los grupos se juntan de acuerdo con la distancia mínima entre las observaciones.
Este tipo de vinculación favorece la homogeneidad de los elementos de cada grupo en detrimento de la diferenciación.

Vinculación completa :
Los grupos se forman de acuerdo a la mínima distancia máxima entre los puntos, por lo que primero se calculan las distancias máximas entre los grupos y luego se eligen aquellas con la menor distancia.
Este tipo de vínculacion resalta más las diferencias entre los grupos que la homogeneidad interna.

Vinculación media (o promedio) :
Los grupos se forman de acuerdo con la minima distancia media, es decir, primero se calcula la distancia promedio entre todas las observaciones y luego entre esas distancias elegimos la la distancia mínima.
Este tipo de vinculación es menos sensible a los valores extremos, por lo que será más robusta.

Distancia de Fusión y Dendograma 
Después de elegir la vinculación más apropiada para tu análisis y crear grupos, se puede generar una representación gráfica llamada dendograma .
Un dendograma representa el nivel de agregación de los clusters ordenados de forma creciente.
Los individuos están en el eje X y las distancias en el eje Y. |
 |
La distancia entre clusters tiende a aumentar y por ello elegimos una regla de parada que nos permita elegir el número de grupos o clusters que queremos tener .
Para ello utilizamos la técnica de tala de árboles:
- Mira las ramas más largas ;
- Emplea el criterio de parsimonia (normalmente 4-5 clusters homogéneos quedarán dentro y los clusters heterogéneos quedarán fuera);
- Mira el diagrama de sedimentación o scree plot basado en las distancias de fusión (corta cuando la gráfica se aplana, o si en la transición del grupo g al grupo g+1 se oblserva un fuerte aumento);
- Cuida que no haya valores atípicos o outliers (en cuyo caso los clústers deberían estar formados por un solo individuo, una única observación) .
Caso de estudio con R
Creando la Matriz de Distancia 
Después de importar la base de datos a R, empezamos el análisis cluster:
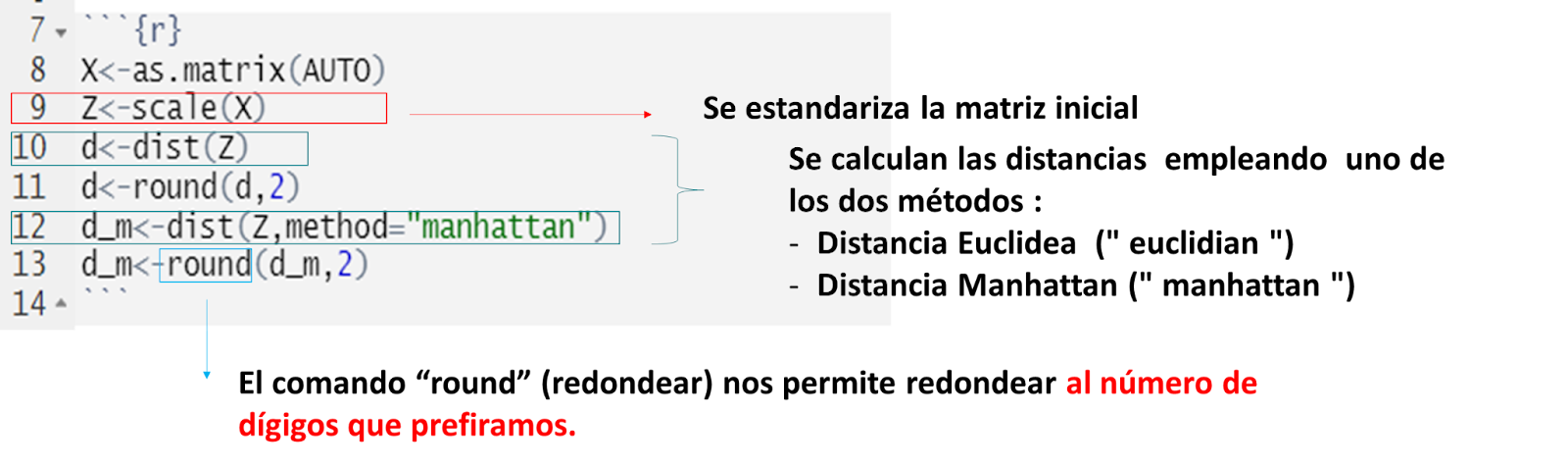
Elegir el tipo de vinculación 
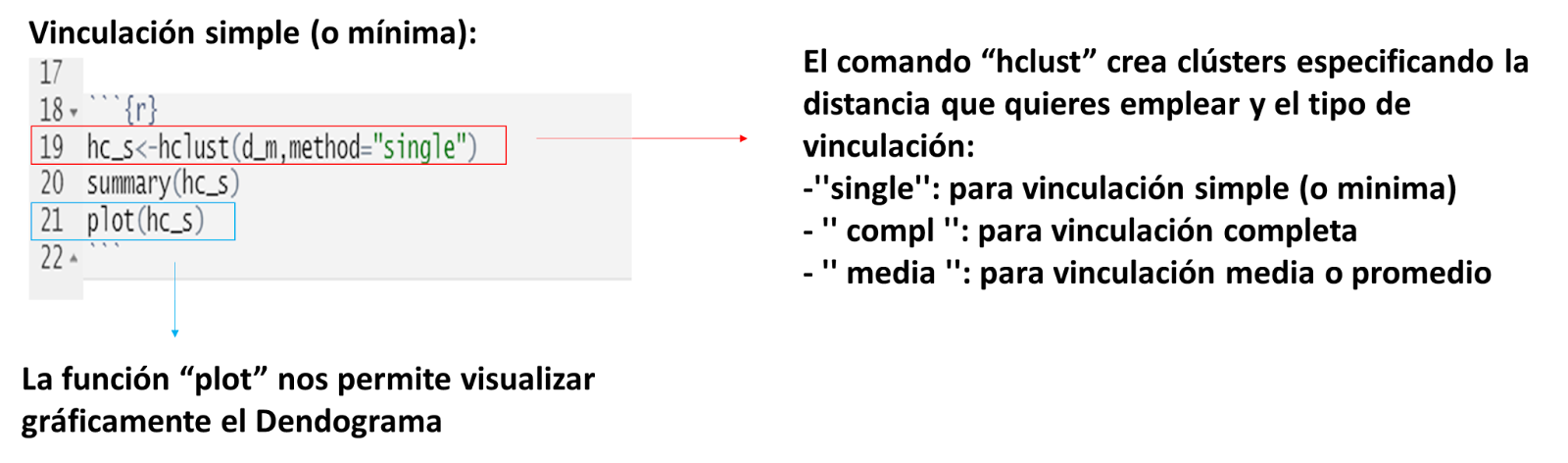


El resultado obtenido con la vinculación simple es:

Se realiza el mismo procedimiento pero con vinculación completa y vinculación promedio.
Ahora tienes que comparar los resultados y elegir la vinculación más representativa para el análisis que estamos realizando.

Comparando las tres vinculaciones, la más adecuada es la vinculación completa, ya que divide mejor los clústers evitando que haya demasiada homogeneidad interna a expensas de la heterogeneidad externa. También evita la formación de valores atípicos (outliers) , es decir, grupos compuestos por un solo individuo.
|


















